The histogram is an approximation of the distribution of numerical data. Karl Pearson was the first to coin the phrase.
It is frequently used to depict the major features of data distribution in a handy format.
Table of Contents
What Is a Histogram?
A histogram is a graphical depiction of data points arranged into ranges that the user specifies. The historical diagram, which resembles a bar graph in appearance, condenses a data series into an easily read visual by grouping many data points into logical ranges or bins.
Important Takeaways
- A historical diagram is a data representation that looks like a bar graph that bins a variety of classifications into columns along the horizontal x-axis.
- The vertical y-axis shows the number or percentage of occurrences in the data for each variable.
- Columns can be used to visualize data distribution patterns.
- Technical analysts utilize the MACD histogram to show variations in momentum in trading. The MACD historical diagram columns can provide buy and sell signals earlier than the MACD and signal lines.
What is Histogram Chart?
A histogram is a type of graphic that divides numerical data into bins and displays the bins as segmented columns.
They are used to represent a dataset’s distribution: how frequently values fall into ranges.
Google Charts will select the number of bins for you.
What is Symmetric Histogram?
A symmetric histogram is one in which the mean and median are equal.
A line drawn through the center of a symmetric historical diagram divides it into two equal halves.
The two parts will be mirror images of one another.
The skewness of a symmetric historical diagram is zero (no skewness)
Historical diagram s are based on area rather than bar height.
The area of the bar in a historical diagram indicates the frequency of occurrences for each bin.
This means that the height of the bar does not always show the number of occurrences of scores within each specific bin.
The frequency of occurrences within a bin is determined by multiplying the height by the width of the bin.
One of the reasons that the height of the bars is sometimes misinterpreted as representing frequency rather than the area of the bar is that many historical diagram contain equally spaced bars (bins), and in these cases, the height of the bin does reflect the frequency.
How Histograms Work
Histograms are frequently used in statistics to show how many of a particular type of variable occur within a given range.
For example, a census focused on a town’s demographics may use a historical diagram to illustrate how many individuals are between the ages of zero and ten, eleven to twenty, twenty to thirty, thirty to forty, forty to fifty, fifty to sixty, sixty to seventy, and seventy to eighty.
Let us suppose that the numbers along the vertical access represent thousands of people.
To read this histogram example, begin with the horizontal axis and notice that there are around 500 people in the town ranging in age from less than one year to ten years.
There are 4,000 people in town between the ages of 11 and 20.
And so forth. Analysts can customize historical diagram in a variety of ways.
They have the ability to alter the interval between buckets.
In the preceding example, there are eight buckets with intervals of ten.
This might be modified to four buckets with a 20-second interval.
Redefining the y-axis is another option to personalize a histogram.
The frequency of occurrences noticed in the data is the most basic label employed.
However, proportion of total or density could also be used instead.
Histograms vs. Bar Charts
Histograms and bar charts both use columns to produce a visual display, and the phrases are frequently used interchangeably.
However, a historical diagram technically shows the frequency distribution of variables in a data set.
A bar graph is a graphical representation of a comparison of discrete or categorical variables.
Create a Histogram
To make a histogram, divide your data into equal-sized pieces known as bins.
These bins are then plotted on a graph, with the height of the bins representing the number of values included within them.
If your data is ordinal or nominal scaled, a histogram is not an option; instead, make a bar chart.
Try it out, it’s simple with Histogram Maker!
You can, of course, plot the normal distribution in your historical diagram.
Under Settings, you can also modify the colors and typefaces of the historical diagram
Using the Histogram tool associated with the Statistical icon in Microsoft Excel, you may build a historical diagram.
Histogram Example: The MACD Histogram
The moving average convergence divergence (MACD) historical diagram is a well-known example of a historical diagram for technical traders.
It’s a well-known technical indicator that shows the difference between the MACD and signal lines.
For example, if the difference between two lines is $5, the MACD historical diagram graphically shows this difference. The MACD historical diagram is placed on a chart to help traders determine the momentum of a given security.
When the MACD line is above the signal line, the historical diagram bar is positive; when the MACD line is below the signal line, the historical diagram bar is negative. An expanding MACD histogram represents a rise in upward momentum, whereas a falling historical diagram represents a decrease in downward momentum.
Trading With the MACD Histogram
The lagging nature of the signal provided is a disadvantage of using only the MACD line and signal line. When the MACD line crosses over the signal line, the trading signal lags behind the price.
Because the two lines are moving averages, they do not cross until a price change has happened.
This means that traders forego part of their first move.
When using the MACD indicator to make trading decisions, traders should not disregard the MACD historical diagram.
By generating earlier entry indications, the MACD historical diagram helps to decrease signal latency.
The length of the historical diagram bars as they move away from the zero line can be tracked by traders.
For example, they may believe that a histogram bar is creating a trade signal if it is shorter in length than the prior bar.
Traders may open a position in the direction of the historical diagram’s decrease once the smaller historical diagram bar has completed.
To boost the signal’s reliability, other technical indicators should be employed in conjunction with the MACD historical diagram.
Furthermore, traders should use a stop-loss order to exit the trade if the security’s price does not move as expected.
What Is a Histogram in Simple Terms?
A histogram is a graph that uses rectangles to represent the frequency of numerical data.
The distribution frequency of a variable is represented by the height of a rectangle (the vertical axis) (the amount, or how often that variable appears).
The variable’s value is represented by the width of the rectangle (horizontal axis) (for instance, minutes, years, or ages).
What Is the Difference Between a Histogram and a Bar Graph?
The distribution frequency is displayed as a two-dimensional figure in the historical diagram, which means that the height and breadth of columns or rectangles have specific meanings and can both vary. A bar chart is a one-dimensional illustration. Its bar heights reflect anything specific. The width of the bars is meaningless. There are no gaps between columns on a historical diagram. The width of the column adjusts as the variable represented changes. Bar charts typically have gaps between them.
When Should a Histogram Be Used?
In general, a historical diagram can be used to represent a comparison of the distribution of particular numerical data in distinct interval ranges. Historical diagram examples can assist an audience in quickly and simply seeing and understanding crucial meanings and patterns associated to a vast amount of data.
They can help a company’s or organization’s decision-making process in numerous departments.
How do you construct a histogram from a continuous variable?
To create a historical diagram from a continuous variable, first divide the data into intervals known as bins.
Age has been divided into bins in the above example, with each bin indicating a 10-year period beginning at 20 years.
The number of occurrences of scores in the data set that are contained within that bin is stored in each bin.
The frequencies in each bin, as well as the scores that contributed to the frequency in each bin, have been tabulated for the aforementioned data set (see below):
| Bin | Frequency | Scores Included in Bin |
| 20-30 | 2 | 25,22 |
| 30-40 | 4 | 36,38,36,38 |
| 40-50 | 4 | 46,45,48,46 |
| 50-60 | 5 | 55,55,52,58,55 |
| 60-70 | 3 | 68,67,61 |
| 70-80 | 1 | 72 |
| 80-90 | 0 | – |
| 90-100 | 1 | 91 |
There are no “gaps” between the bars, unlike a bar chart (although some bars might be “absent” reflecting no frequencies).
Because a historical diagram shows a continuous data collection, there are no gaps in the data (although you will have to decide whether you round up or round down scores on the boundaries of bins).
Histogram Graph
A histogram graph is a data representation in the form of a bar graph.
It is a representation of a variety of outcomes in the form of columns arranged along the x-axis.
The y-axis of the same historical diagram represents the number count or multiple occurrences in the data for each column.
It is the simplest method for visualizing data distributions.
You can learn about historical diagram graphs by plotting one for the example given below.
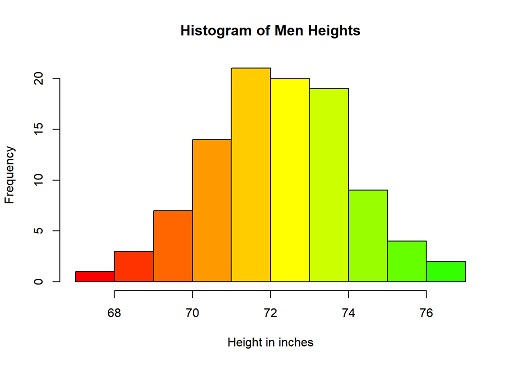
Uncle Bruno has 30 black cherry trees in his garden.
Each tree is varied in height.
The tree heights (in inches) are as follows: 61, 63, 64, 66, 68, 69, 71, 71.5, 72, 72.5, 73, 73.5, 74, 74.5, 76, 76.2, 76.5, 77, 77.5, 78, 78.5, 79, 79.2, 80, 81, 82, 83, 84, 85, 87.
By specifying a range, we may group the data in a frequency distribution table as follows:
| Height Range (ft) | Number of Trees (Frequency) |
| 60 – 75 | 3 |
| 66 – 70 | 3 |
| 71 – 75 | 8 |
| 76 – 80 | 10 |
| 81 – 85 | 5 |
| 86 – 90 | 1 |
A historical diagram can now be used to display this data. We must ensure that there are no gaps between the bars when plotting a historical diagram.
How to Make a Histogram?
The following steps demonstrate how to create a histogram from the given data:
- Select an appropriate scale to represent weights on the horizontal axis.
- Select an appropriate scale to display the frequencies on the vertical axis.
- Using the frequencies of the specified weights, draw the bars that correspond to them.
- Create a histogram for the following frequency distribution table, which describes the weight frequencies of 25 individuals in a class.
| Weights (in lbs) | Frequency (Number of students) |
| 65 – 70 | 4 |
| 70 – 75 | 10 |
| 75 – 80 | 8 |
| 80 – 85 | 4 |
Steps To Draw a Histogram
- On the horizontal axis, set the scale to 1 unit = 11 lb. Because the weights in the table begin at 65, rather than 0, we provide a break/kink on the X-axis.
- The frequencies on the vertical axis range from 4 to 10. As a result, we used a scale of 1 unit = 2.
- Using the frequencies of the specified weights, draw the bars that correspond to them.
Frequency Histogram
A frequency histogram is a historical diagram that displays the frequencies (number of occurrences) of data objects.
In a hospital, for example, there are 20 newborn newborns whose ages are listed in ascending order as follows:
1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 5.
This data can be represented in a frequency distribution table as follows:
| Age (in days) | Frequency |
| 1 | 4 |
| 2 | 5 |
| 3 | 8 |
| 4 | 2 |
| 5 | 1 |
A frequency histogram can now be used to display this data.
How to Draw Histogram For Grouped Data
The bars in a historical diagram are displayed continuously side by side, with no gaps between them.
That is, in a historical diagram, rectangles are built on the distribution’s class intervals.
The rectangle’s areas are proportional to the frequencies.
Let’s have a look at the procedures involved in creating a historical diagram for grouped data.
- If the data is in the discontinuous (inclusive) form, represent it in the continuous (exclusive) form.
- Draw the class intervals on a uniform scale along the X-axis.
- Draw a uniform scale of frequencies along the Y-axis.
- Make rectangles with class intervals as bases and frequencies as heights.
Histogram Shapes
Based on the frequency distribution of the data, the histogram can be categorized into distinct categories.
Normal distribution, skewed distribution, bimodal distribution, multimodal distribution, comb distribution, edge peak distribution, dog food distribution, heart cut distribution, and so on are all examples of distributions.
These various sorts of distributions can be represented by the historical diagram.
There are primarily five types of historical diagram shapes.
They are as follows:
- Bell Shaped Histogram
- Bimodal Histogram
- Skewed Right Histogram
- Skewed Left Histogram
- Uniform Histogram
Let us go over the various forms of h historical diagram or histogram shapes in further depth using practical examples.
Bell-Shaped Histogram
A histogram with a bell shape has a single peak.
The historical diagram has only one peak at this time interval, indicating that it is bell-shaped.
This historical diagram features a single peak.
Bimodal Histogram
A bimodal historical diagram has two peaks
Skewed Right Histogram
A right-skewed historical diagram is one that is skewed to the right.
The bars in this historical diagram are skewed to the right, giving rise to the term “skewed right historical diagram.
Skewed Left Histogram
A historical diagram that is skewed to the left is known as a skewed left historical diagram.
The bars in this historical diagram are skewed to the left, giving rise to the term “skewed left historical diagram.
Uniform Histogram
A uniform histogram is one in which all of the bars have around the same height.
Histogram Calculator
A historical diagram calculator is a free online application that displays a historical diagram for a given set of data. You can enter the intervals and frequency from the data into the calculator, and the historical diagram for that data will be displayed in a few seconds.
Histogram Hints & Tips
The following are a few crucial guidelines and tricks to remember while visualizing any data with a historical diagram.
- When generating a historical diagram, select the scale on the vertical axis and look for the largest number that divides all the frequencies.
- If no such number exists, look for the greatest number that splits the majority of the frequencies.
- A historical diagram is a graph that summarizes continuous data.
- A historical diagram provides a visual explanation of continuous data.
- The scales of both the horizontal and vertical axes do not have to begin at zero.
- A historical diagram should have no gaps between its bars.
FAQs
What is a histogram and why is it used?
A popular graphing tool is the historical diagram.
It is used to summarise discrete or continuous data on an interval scale.
It is frequently used to depict the major features of data distribution in a handy format.
How can I create a histogram in Excel?
Insert > Chart is the option.
Click historical diagram under All Charts in the Insert Chart dialog box, then OK.
How do you make a histogram and line graph on Excel?
To make a Histogram chart in Excel 2016, follow these steps:
- Choose the complete dataset.
- Navigate to the Insert tab.
- In the Charts group, select ‘Insert Static Chart.’
- Select the Histogram chart icon from the HIstogram group.
How do you make a histogram with two sets of data?
The obvious solution is to right-click -> pick data -> add both data series to the chart, however the historical diagram still only displays one set of data.
What is an example of a histogram?
There are 5 clients that are waiting from 1 to 40 seconds. There are 5 clients that are waiting from 1 to 45 seconds. There are 5 clients that are waiting from 1 to 50 seconds. There are now two customers that are waiting between 1 and 55 seconds.
How do you read histograms?
The left side of the graph shows the photo’s blacks or shadows, the right side represents the photo’s highlights or bright parts, and the middle section represents the photo’s midtones. The graph’s peaks represent the number of pixels in a specific tone (with each peak corresponding to a different tonal value).
How do you use a histogram in math?
To interpret a historical diagram, look at the bar, then the x-axis to see what the data represents, and finally the y-axis to see how frequently that particular data happens. If the bar at 7 feet moves up to 8 on the y-axis in the tree height historical diagram, it means I have 8 trees that are 7 feet tall.
